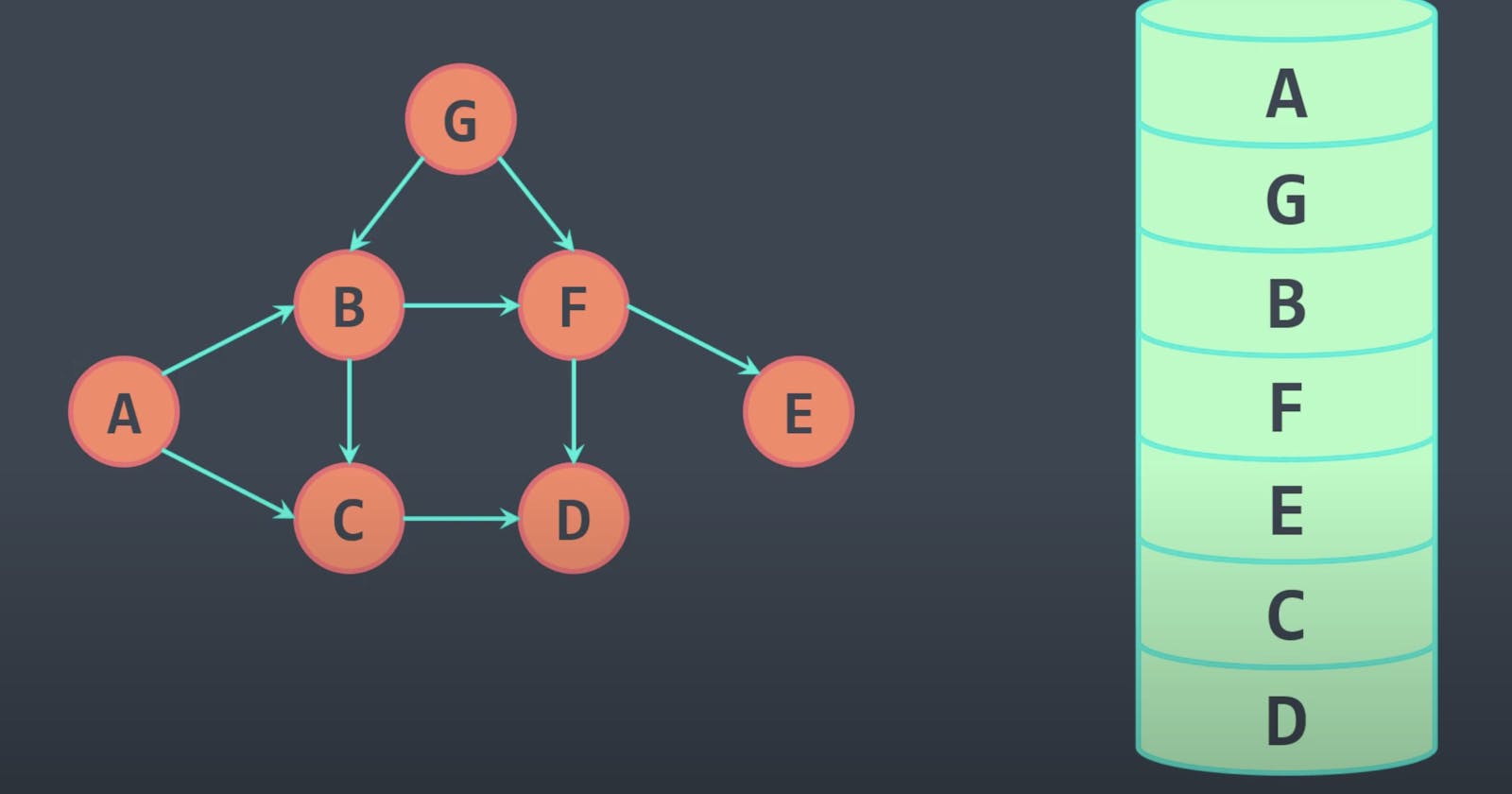
How many times do you get muddled about what sequence of subtasks you should follow to complete a bigger one and wonder if there was a way to find that out? Computer Science is all about taking abstract problems like these and solving them by reducing them to decision problems. For example "finding the order of subtasks" to "if there is a linear order of subtasks".

Graphs are a great way to represent real-world problems like these abstractly so we can apply discrete mathematics and let a computer recognise them. There are majorly two ways to represent graphs in a format that can be recognised by a computer. One is to define a set of nodes and give a set of all other nodes that form an edge with them. The other is to define an n x n 2-dimensional matrix(where n is the number of nodes in the graph), the value of the i x j element of this graph is determined by whether the ith and jth nodes form an edge together or not.

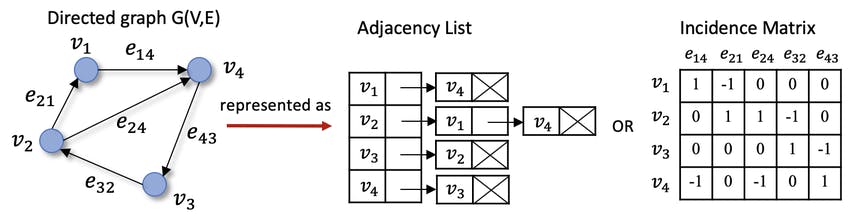
But to solve the problem at hand we need to use a variation of a directed graph, called the directed acyclic graph. We are going to map our subtasks in the form of nodes and all the directed edges pointing to that node will be the ones coming from nodes that are a pre-requisite of that subtask.

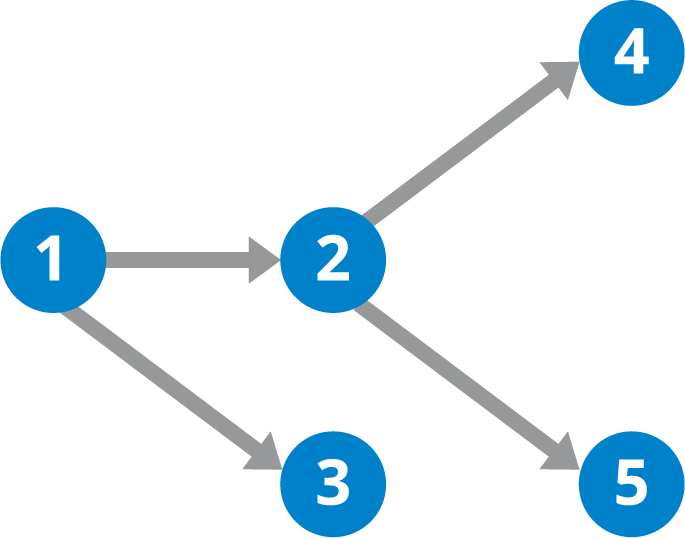
Here's how the topological sort algorithm works:

1. Start by initializing an empty list, which will store the sorted vertices.

2. Choose any vertex in the graph that has no incoming edges (in-degree of 0) and add it to the list. If multiple vertices have no incoming edges, you can choose any of them.

3. Remove the chosen vertex and all its outgoing edges from the graph.

4. Repeat steps 2 and 3 for the remaining graph until no vertices are left.

5. If there are still vertices remaining in the graph after step 4, it means that the graph contains cycles, and a topological ordering is not possible since cycles imply dependencies that cannot be resolved. In such cases, the algorithm terminates without providing a valid topological ordering.

6. If all vertices are successfully added to the list, it represents a valid topological ordering of the graph.

The resulting list obtained from the algorithm is the topological sort of the graph. It represents a linear ordering where each task or event can be performed after all its dependencies have been completed. For the graph given above, the order of events should be 1, 3, 2, 4, 5.

Topological Sort has many applications :

1. Finding cycle in a graph

A topological ordering is possible only for directed acyclic graph(DAG). For a cyclic graph topological ordering is not possible.

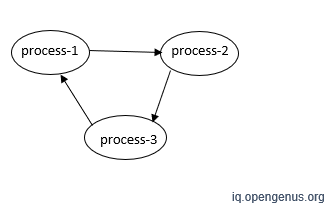
In the figure above (process-1 → process-2), process-2 can be started only when process-1 is already finished. We can say that process-2 depends on process-1, process-3 on process-2, and process-1 on process-3.

If the given graph contains a cycle, then there is at least one vertex will break topological order. If topological sort isn't defined then we can say that the graph is cyclic.

2. Operation System deadlock detection

Deadlock is a state in which a process in a waiting state and another waiting process is holding the demanded resource.

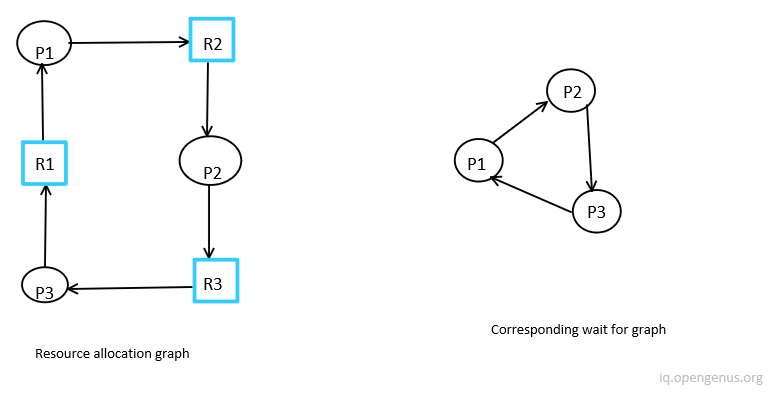
Here, process P1 holds resource R1, process P2 holds resource R2, process P3 holds resource R3, and process P1 is waiting for R2, process P2 is waiting for R3 and process P3 waiting for R1, then process P1, process P2 and process P3 will be in a deadlock. Topological sorting is used here to identify a cycle. If the wait-for graph has a cycle, then there is deadlock.

3. Dependency resolution:

Suppose, A class extends B class. Then B has a dependency on A, and A must be compiled before B.

What happens if A extends B and B also extends A in java? In this
case, the java compiler tries to detect circular dependency.

public class A extends B {
    // some code
}

public class B extends A {
    // some code
}
JavaCopy

Here B is the subclass of A and A is the subclass of B. This relationship is not possible. Java compiler shows an error message.

4. Sentence Ordering:

A set of n documents D={d₁,d₂...,d_n} and the number of sentences in a document is v_i,where ∀i,v_i\>=1. If a random order o=[o₁,....o_vi] and a set of v_i sentences in a random order is {S_o1,S_o2,...,S_ovi}. Then the task is to find the right order of the sentences o*={o*₁,...o*_vi}.
A set of constraints C_i represent the relative ordering between every pair of sentences in d_i where
|C_i|=(v_i×(v_i-1))/2.

For example, if a document has three sentences in the correct order s1 < s2 < s3, then we have three set of constraints {s1 < s2, s1 < s3, s2 < s3}

The order of the sentences can be represented using a DAG. Here the sentences(S_i) represent the vertices, and the edges represent the ordering between sentences.

For example, if we have a directed edge between S₁ to S₂, then S₁ must come before S₂. Topological sort can produce an ordering of these sentences (Sentence ordering).

5. Critical Path Analysis:

Critical path analysis is a project management technique. It is used to find the minimum time a project can take and the dependencies of each activity on others. The completion of the project requires the completion of some activities. An activity may have some predecessor activities. It is mandatory to finish the predecessor activities to start a new activity. The critical path calculates the longest path of the activity graph. Activities represent vertices, and edges represent the preceding relationship between them. Activities are listed in topological order.

The critical path algorithm is also used to find the Hamiltonian path in a DAG. The Hamiltonian path is a path in a graph(undirected or directed graph) that visits each vertex exactly once. If a Hamiltonian path exists, the topological order is unique.

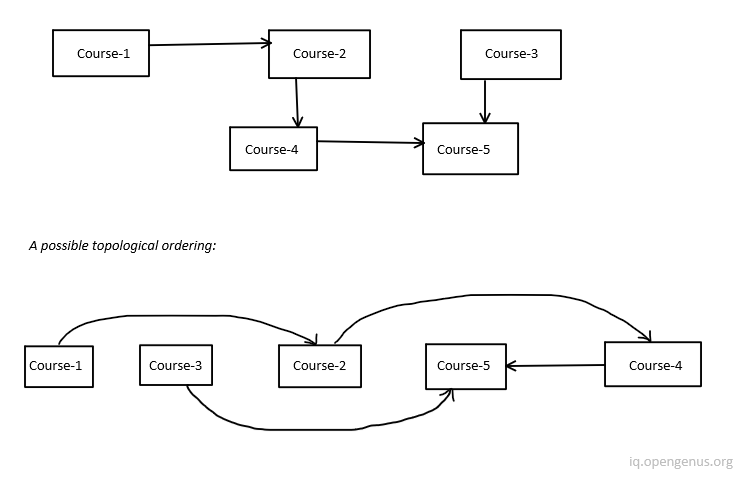
6. Course Schedule problem:

There are some courses and they may have some prerequisite courses. One can finish courses in some order.

Prerequisites of course:

Some other applications of the topological sort are manufacturing workflows, data serialization, context-free grammar and many more.